lohabets.blogg.se - Isosceles triangle side lengths

#Isosceles triangle side lengths how to
#Isosceles triangle side lengths plus

I had never thought about trying to find two rational triangles with the same perimeters and areas before, so I didn’t know how to feel when I found out.

For the isosceles triangle, you can either apply Heron’s formula, which gives you the area of a triangle using only its side lengths, or first find the altitude of the triangle using the Pythagorean theorem and then figure out the area of the triangle from there. Either way you do it, you will find that each triangle’s perimeter is 864 units and area is 23,760 square units.Ī special pair of triangles. Credit: Evelyn Lamb It’s simple to compute the area of a right triangle knowing only its side lengths: it is half of the product of the shorter two sides. If you’re suspicious, you can easily add up the side lengths to see that their perimeters are the same. The right triangle of this pair has side lengths (135, 352, 377), and the isosceles has side lengths (132, 366, 366).

The perimeters and areas of both triangles are equal.

All side lengths of both triangles are rational numbers, and.

One triangle is a right triangle and one is isosceles,.

Heron’s formula states that the area T is equal to the square root of the semiperimeter s times semiperimeter s minus leg a times semiperimeter s minus a times semiperimeter s minus base b.In all the (Euclidean) world, up to simple scaling, there is only one pair of triangles with the following properties: The semiperimeter s is equal to half the perimeter. Given the perimeter you can solve the semiperimeter.

#Isosceles triangle side lengths plus

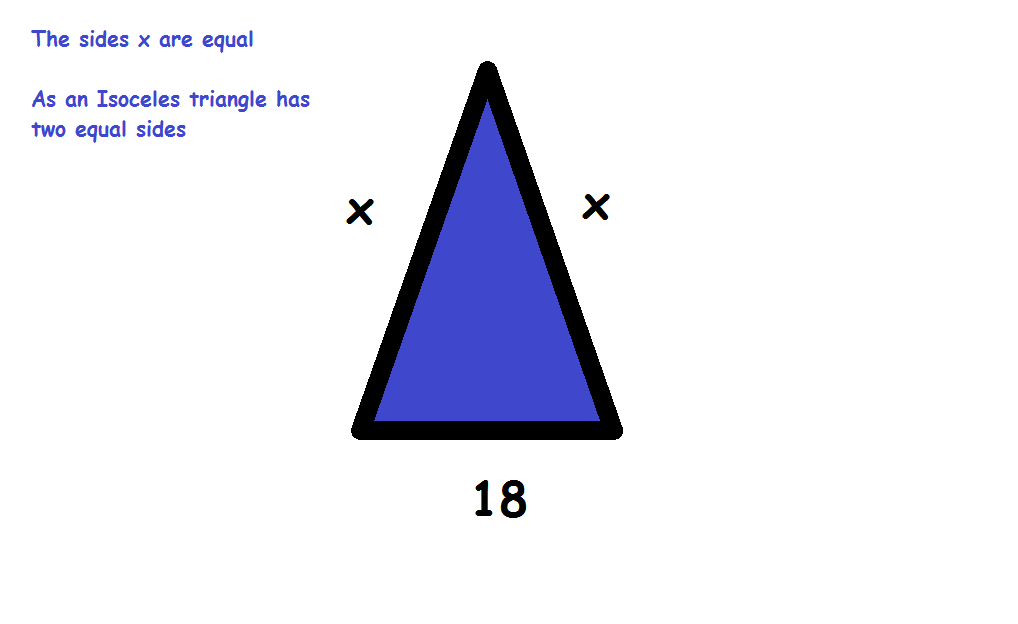
Thus, the perimeter p is equal to 2 times leg a plus base b. Solve the perimeter of an isosceles triangle using the following formula: Given the sides of an isosceles triangle it is possible to solve the perimeter and area using a few simple formulas. The vertex angle β is equal to 180° minus 2 times the base angle α. Use the following formula to solve the vertex angle: The base angle α is equal to 180° minus vertex angle β, divided by 2. Use the following formula to solve the base angle: Given any angle in an isosceles triangle it is possible to solve the other angles. How to Calculate the Angles of an Isosceles Triangle The leg length a is equal to the square root the height h squared plus the base b divided by 2, squared. Use the following formula to solve the length of the legs: The base length b is equal to 2 times the square root of leg a squared minus the height h squared. Use the following formula to solve the length of the base edge: Given the height, or altitude, of an isosceles triangle and the length of one of the legs or the base, it’s possible to calculate the length of the other sides. How to Calculate Edge Lengths of an Isosceles Triangle We have a special right triangle calculator to calculate this type of triangle. Try our equilateral triangle calculator.Ī right isosceles triangle is a triangle with a vertex angle equal to 90°, and base angles equal to 45°. An equilateral triangle is a special case where all the angles are equal to 60° and all three sides are equal in length.

There are four types of isosceles triangles: acute, obtuse, equilateral, and right.Īn acute isosceles triangle is a triangle with a vertex angle less than 90°, but not equal to 60°.Īn obtuse isosceles triangle is a triangle with a vertex angle greater than 90°.Īn equilateral isosceles triangle is a triangle with a vertex angle equal to 60°.